Supporting Unfinished Learning in Math
In my last post, I shared that supporting unfinished learning requires complex and unsexy work and that we risk harm when we try to oversimplify the task.
This week, we start a tour of real examples from different disciplines about what it takes to support unfinished learning well. We’ll start with math.
Too often math is treated like a linear sequence of learning or a checklist of skills. What I learned from conversations with math experts and practitioners led me to think about teaching math like helping students build a house. Some walls are load-bearing and need to be strong before moving up a level; other walls can be useful for connections but should not be considered prerequisites.
Let’s trace a fourth-grade math example. Fourth grade has some big and important concepts—multiplication and division of whole numbers, really getting into fraction equivalence—while making connections to geometric shapes and area concepts. There are some load-bearing walls for multiplication and division (things like place value and fluency with addition and subtraction).
So what do teachers really need to do to support this learning?
We worked with several districts this year to test different approaches and found a series of key instructional moves needed in the year-long plan, in the unit plan, and at the lesson level. I’m going to walk through the learnings below, but I also put together a video that you can watch here:

Looking at the year . . .
1. Up front, teachers need a strong understanding of the arc of the year.
2. Teachers need to identify which units/modules focus on this priority content. Student Achievement Partners released helpful priority content guidance to support this identification. For example, in the fourth-grade EngageNY units, modules 1, 3, 5, and 6 contain more than 50% priority content:
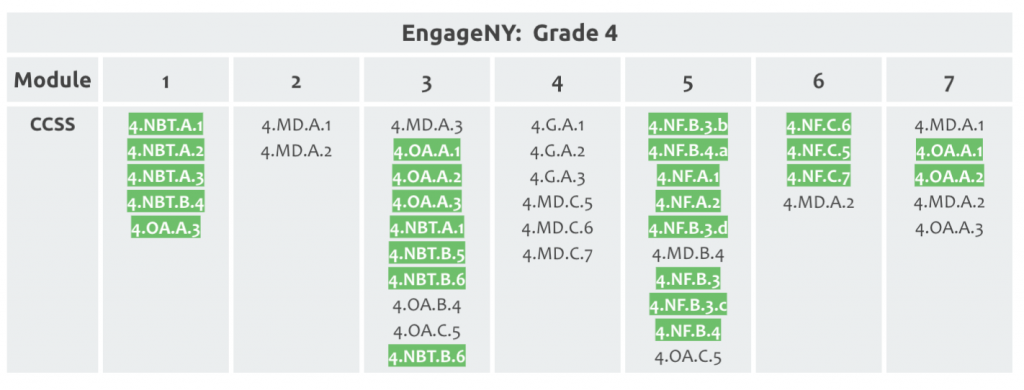
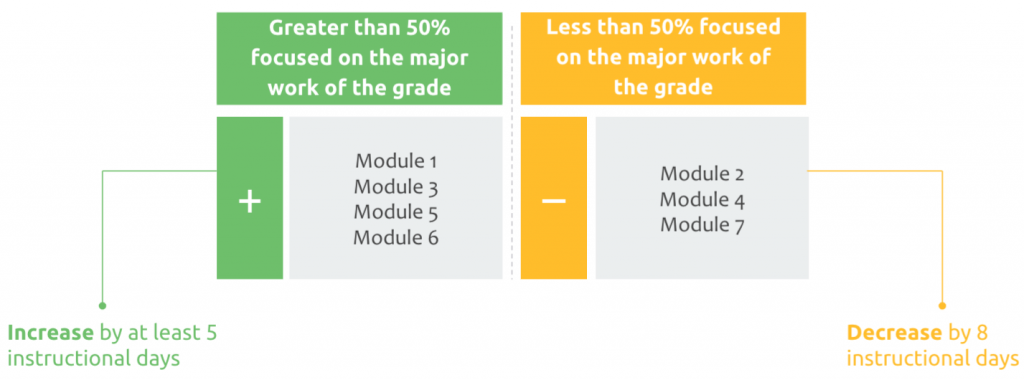
3. Teachers need to create MORE time in the units/modules with priority content to support unfinished learning. They do this by looking at where other units can be streamlined. For example, teachers need more time for module 3 (multiplication/division) and module 5 (fractions). This time can be found by merging lessons in modules 2 (metric conversions) and 6 (decimals).
Looking at a unit/module . . .
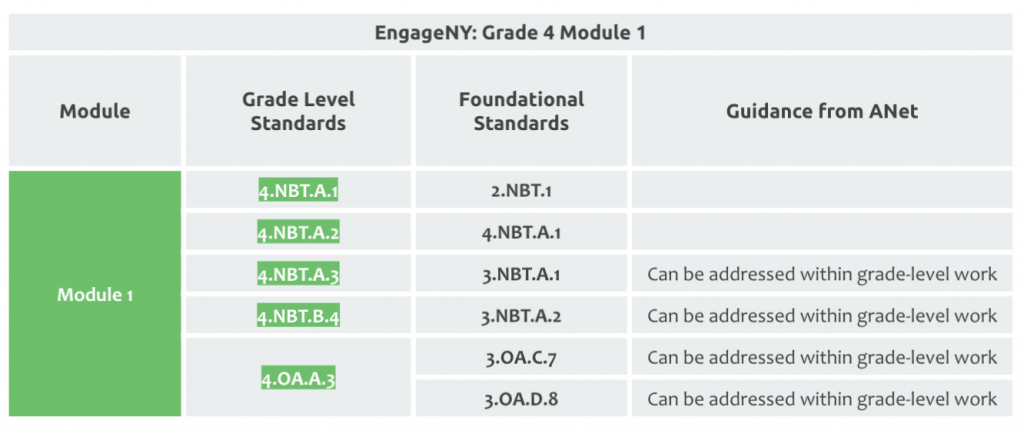
4. Teachers need to understand the story of the unit/module. For example, module 1 of fourth-grade math in EngageNY focuses on addition and subtraction with whole numbers.
5. Teachers need to understand the load-bearing walls for the grade-level standards in that unit/module. To be ready for module 1, students need an understanding of how to add and subtract using place value and some key problem-solving strategies (e.g., how to use a number line).
6. Teachers need to develop/select pre-unit assessment questions aligned to those load-bearing standards. This is not a pre-test/post-test, but rather a couple of targeted, open-ended questions on the prerequisite load-bearing walls.

Moving into the unit/module . . .
7. Teachers need to review student work from the pre-unit assessment. This shows them which load-bearing concepts and strategies students know and which will need support in order for students to be able to access the grade-level content.
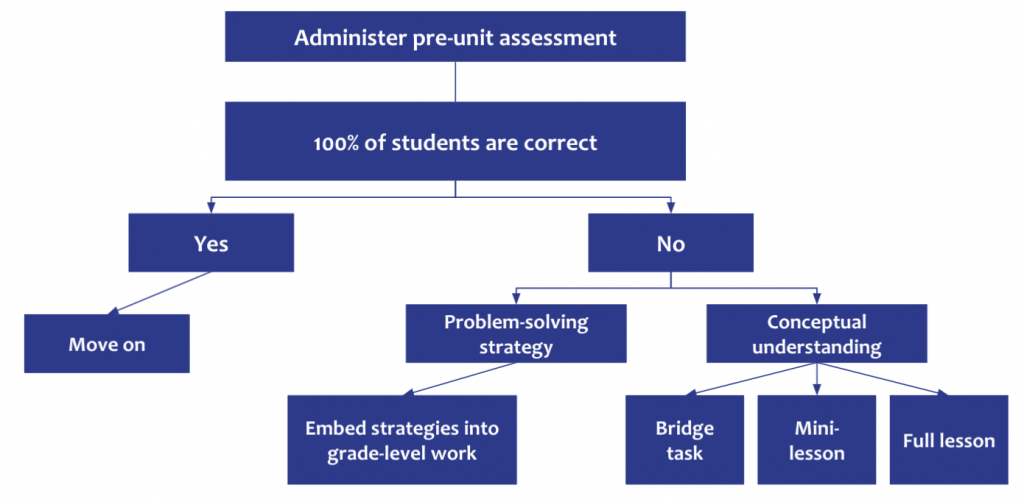
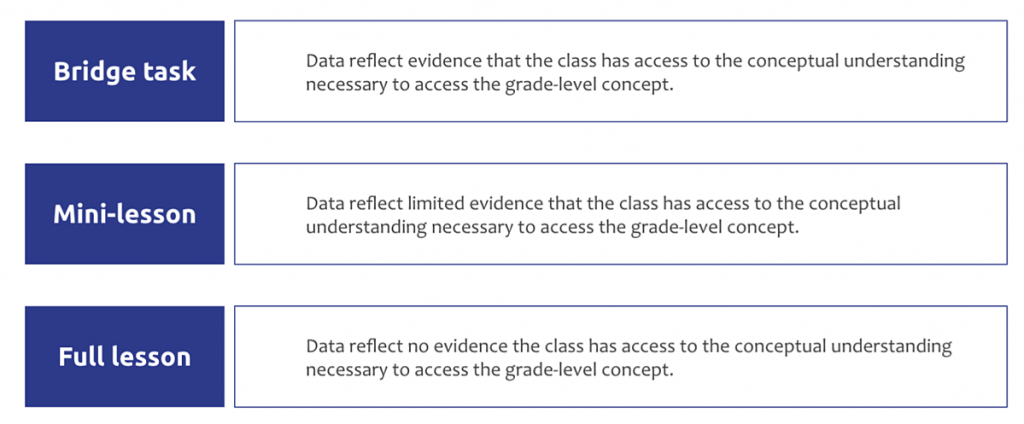
8. If students need support to access the grade-level content, teachers can plan to use the extra time they already created to support access. This can be done with a bridge task, a mini lesson, or a full lesson (for example, find the third-grade lesson on the key load-bearing concept and teach it the day before).
What you do NOT see in this approach is a full unit of third-grade learning before starting fourth-grade work. In mathematics, unfinished learning is better supported when embedded within the relevant grade-level units.
Complex? Yes. Impossible? No.
This is the work good teaching always requires. It takes time and focus and patience to prepare for the year and prepare for each unit/module.
Here are the resources we used in this example:
- The video walkthrough
- The Google Slides we used in our walkthrough
- Student Achievement Partners’ Priority Content and Coherence Map
- Achievement Network’s Important Prerequisite Math Standards
- UnboundEd’s version of the EngageNY Math curriculum
Instruction Partners will be testing additional support approaches, especially within the unit launch, this summer and throughout next year, and we will share as we go. (If you or someone you know wants to sign up for these resources, click here.)
And remember: What works in math does not necessarily apply to other disciplines.
Up next: science.
Credit where credit is due: This work was driven by Instruction Partners team members Cammie Mabry, Melissa Chipman, Molly Shields, Rebecca Few, Julia Dezen, Carla Seeger, and Kelsey Hendricks.


